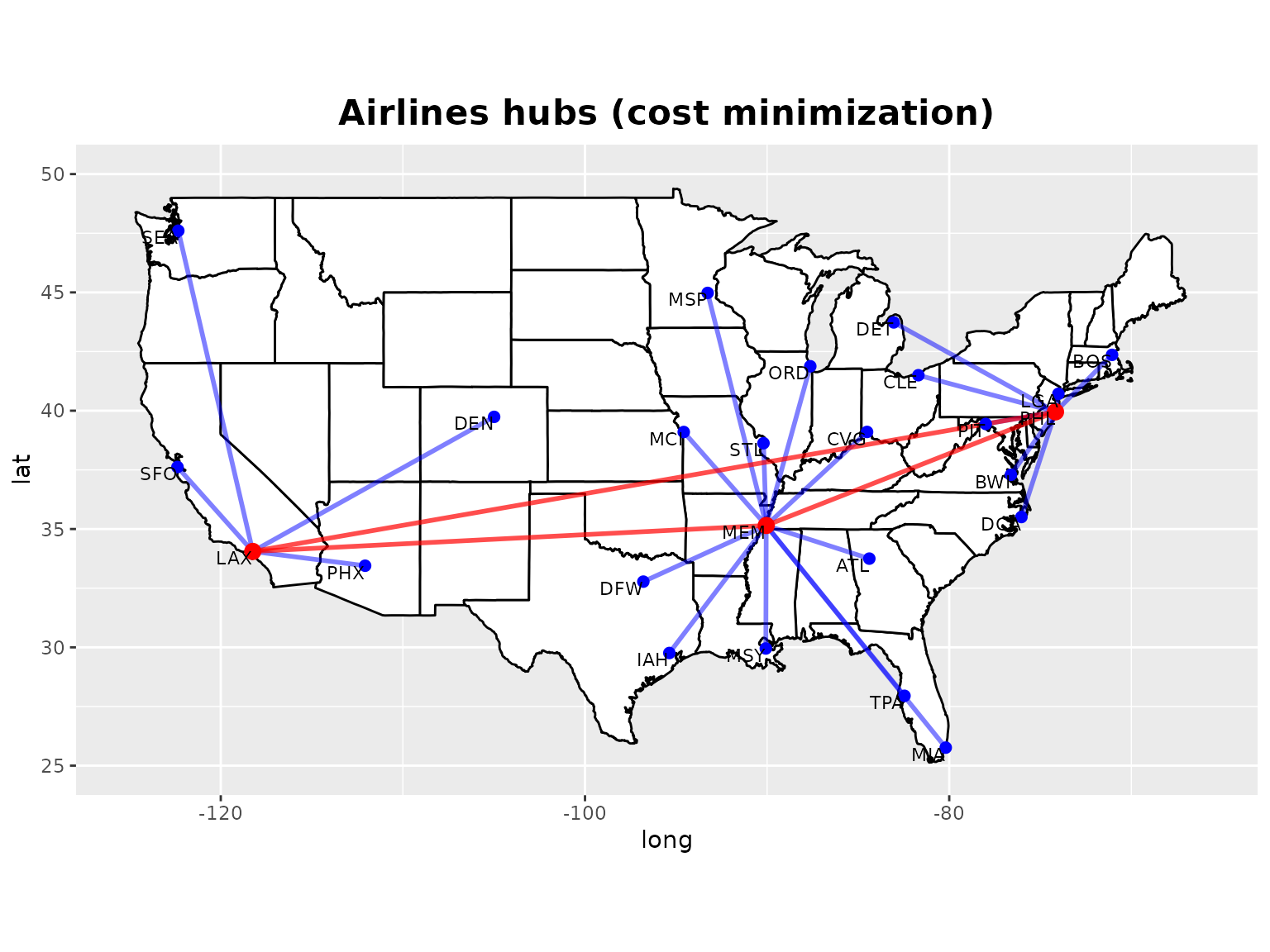
Airline hubs

In this example, we show how, With the Quantum Genetic Algorithm, it is possible to determine the most convenient hubs, given a set of 25 USA airports.

Prepare data

As input data, we consider the 25 airports, with their geographical coordinates:

cities <- read.csv("Airlines_cities.csv")
print(cities)
#>    ID City     Lat      Long
#> 1   1  ATL 33.7490  -84.3880
#> 2   2  BWI 37.2904  -76.6122
#> 3   3  BOS 42.3601  -71.0589
#> 4   4  ORD 41.8781  -87.6298
#> 5   5  CVG 39.1031  -84.5120
#> 6   6  CLE 41.4993  -81.6944
#> 7   7  DFW 32.7767  -96.7970
#> 8   8  DEN 39.7392 -104.9903
#> 9   9  DET 43.7314  -83.0458
#> 10 10  IAH 29.7604  -95.3698
#> 11 11  MCI 39.0997  -94.5786
#> 12 12  LAX 34.0522 -118.2437
#> 13 13  MEM 35.1495  -90.0490
#> 14 14  MIA 25.7617  -80.1918
#> 15 15  MSP 44.9778  -93.2650
#> 16 16  MSY 29.9511  -90.0715
#> 17 17  LGA 40.7128  -74.0060
#> 18 18  PHL 39.9526  -74.1652
#> 19 19  PHX 33.4484 -112.0740
#> 20 20  PIT 39.4406  -77.9959
#> 21 21  STL 38.6270  -90.1994
#> 22 22  SFO 37.6213 -122.3790
#> 23 23  SEA 47.6062 -122.3321
#> 24 24  TPA 27.9506  -82.4572
#> 25 25  DCA 35.5072  -76.0369

In addition, we get two square matrices. The first one contains the costs:

cost <- read.csv("Airlines_cost.csv",header=F)
str(cost)
#> 'data.frame':    25 obs. of  25 variables:
#>  $ V1 : num  0 577 946 598 374 ...
#>  $ V2 : num  577 0 370 613 429 ...
#>  $ V3 : num  946 370 0 858 750 ...
#>  $ V4 : num  598 613 858 0 255 ...
#>  $ V5 : num  374 429 750 255 0 ...
#>  $ V6 : num  560 313 556 311 226 ...
#>  $ V7 : num  709 1196 1541 790 794 ...
#>  $ V8 : num  1208 1502 1765 907 1080 ...
#>  $ V9 : num  604 406 621 237 239 ...
#>  $ V10: num  695 1242 1603 932 880 ...
#>  $ V11: num  681 960 1251 406 533 ...
#>  $ V12: num  1937 2318 2600 1742 1890 ...
#>  $ V13: num  332 787 1137 486 402 ...
#>  $ V14: num  593 950 1267 1187 947 ...
#>  $ V15: num  909 939 1125 346 599 ...
#>  $ V16: num  426 1000 1368 830 700 ...
#>  $ V17: num  756 179 190 720 578 ...
#>  $ V18: num  672.6 96.3 274.3 675.3 512.4 ...
#>  $ V19: num  1590 2000 2299 1447 1571 ...
#>  $ V20: num  527 211 494 404 256 ...
#>  $ V21: num  483 736 1043 256 307 ...
#>  $ V22: num  2141 2456 2703 1854 2036 ...
#>  $ V23: num  2184 2340 2504 1733 1967 ...
#>  $ V24: num  408 844 1189 1006 775 ...
#>  $ V25: num  540.7 36.5 405.8 592 399.2 ...

that is, for each origin airport, the unit cost (the price of the ticket), necessary to reach the destination airport.

The second one is related to the flows:

flow <- read.csv("Airlines_flow.csv",header=F)
str(flow)
#> 'data.frame':    25 obs. of  25 variables:
#>  $ V1 : num  0 6469 7629 20036 4690 ...
#>  $ V2 : num  6469 0 12999 13692 3322 ...
#>  $ V3 : num  7629 12999 0 35135 5956 ...
#>  $ V4 : num  20036 13692 35135 0 19094 ...
#>  $ V5 : num  4690 3322 5956 19094 0 ...
#>  $ V6 : num  6194 5576 14121 35119 7284 ...
#>  $ V7 : num  11688 3878 5951 21423 3102 ...
#>  $ V8 : num  2243 3202 5768 27342 1562 ...
#>  $ V9 : num  8857 6699 16578 51341 7180 ...
#>  $ V10: num  7248 4198 4242 15826 1917 ...
#>  $ V11: num  3559 2454 3365 28537 2253 ...
#>  $ V12: num  9221 7975 22254 65387 5951 ...
#>  $ V13: num  10099 1186 1841 12980 1890 ...
#>  $ V14: num  22866 7443 23665 44097 7097 ...
#>  $ V15: num  3388 1162 6517 51525 2009 ...
#>  $ V16: num  9986 5105 3541 14354 1340 ...
#>  $ V17: num  46618 24817 205088 172895 25303 ...
#>  $ V18: num  11639 6532 37669 37305 6031 ...
#>  $ V19: num  1380 806 2885 15418 1041 ...
#>  $ V20: num  5261 8184 13200 26221 4128 ...
#>  $ V21: num  5985 3896 7116 42303 5452 ...
#>  $ V22: num  6731 7333 17165 35303 3344 ...
#>  $ V23: num  2704 3719 4284 13618 1067 ...
#>  $ V24: num  12250 2015 8085 17580 4608 ...
#>  $ V25: num  16132 565 51895 40708 7050 ...

that is, for each origin airport, the estimated number of passengers that want to reach the destination airport.

Optimization

We want to minimize the total cost of the optimal solution, given by the product of the flows muliplied by the unit cost, to determine which could be the three more convenient hubs for the 25 airports.

We define the fitness function consequently:

airline_hub <- function(solution,input) {
  cost <- input$cost
  flow <- input$flow
  penalization <- sum(cost)*0.0005
  obj <- -sum(apply(cost[,solution] * flow[,solution], 1, min)) / sum(cost)
  if (length(table(solution)) < length(solution)) {
    obj <- obj - penalization
  }
  # cat("\nSolution:",solution,"  obj: ",obj)
  return(obj)
}

Some remarks:

this function will receive, as input, the cost matrix and the flow matrix;
to evaluate the current solution, in both matrices (cost and flow) we select the three columns corresponding to the three hubs, and calculate the sum of the total costs for each origin airport to reach the candidate hub, selecting the minimum (the minus sign is due to the fact that we want to minimize the value of the objective function);
a penalization is introduced to eliminate the solutions with a number of hubs lower than three.

We can now proceed with the optimization. Note that we set the value of the genome equal to 3 (the number of the desired hubs), and the number of the values to be attributed to each element of the genome is set equal to the number of the airports (25).

input <- list(cost=cost,flow=flow)
popsize = 20
Genome = 3 # Number of desired hubs
nvalues_sol = 25
set.seed(4321)
solutionQGA <- QGA(
                popsize,
                generation_max = 200,
                nvalues_sol,
                Genome,
                thetainit = 3.1415926535 * 0.025,
                thetaend = 3.1415926535 * 0.005,
                pop_mutation_rate_init = 3/(popsize + 1),
                pop_mutation_rate_end = 1/(popsize + 1),
                mutation_rate_init = 3/(Genome + 1),
                mutation_rate_end = 1/(Genome + 1),
                mutation_flag = TRUE,
                plotting = FALSE,
                progress = FALSE,
                verbose = FALSE,
                eval_fitness = airline_hub,
                eval_func_inputs = input,
                stop_iters = 150)
#> 
#>  *** Best fitness:  -69.59383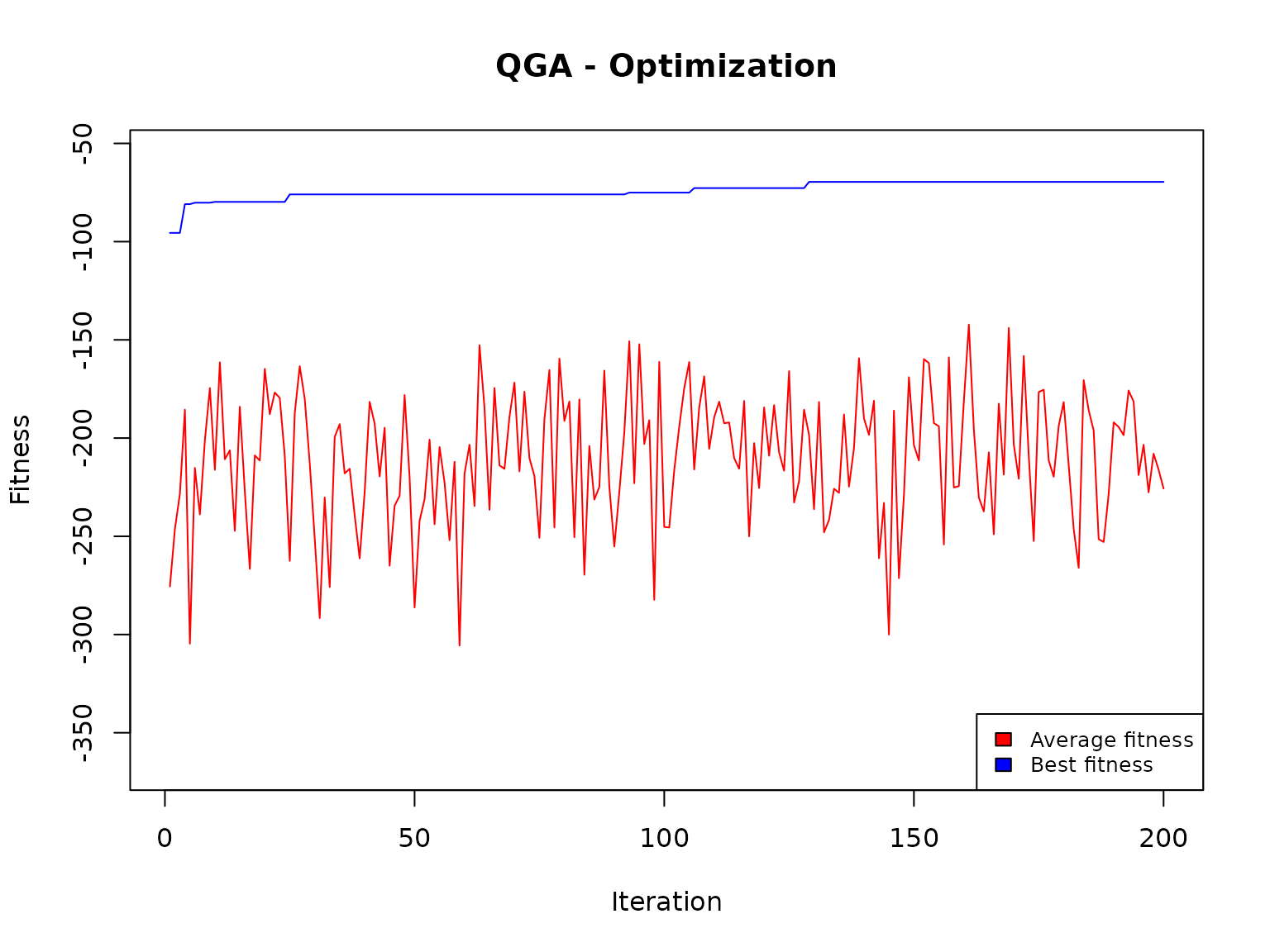

Analysis of the solution

The found solution:

solution <- solutionQGA[[1]]
cities$City[solution]
#> [1] "MEM" "LAX" "PHL"
sol <- cost[,solution] 
find_min_column <- function(row) {
  which.min(row)
}
min_column_vector <- apply(sol, 1, find_min_column)
print(min_column_vector)
#>  [1] 1 3 3 1 1 3 1 2 3 1 1 2 1 1 1 1 3 3 2 3 1 2 2 1 3
cities$Hub <- cities$City[solution][min_column_vector]
print(cities[,c(2,5)])
#>    City Hub
#> 1   ATL MEM
#> 2   BWI PHL
#> 3   BOS PHL
#> 4   ORD MEM
#> 5   CVG MEM
#> 6   CLE PHL
#> 7   DFW MEM
#> 8   DEN LAX
#> 9   DET PHL
#> 10  IAH MEM
#> 11  MCI MEM
#> 12  LAX LAX
#> 13  MEM MEM
#> 14  MIA MEM
#> 15  MSP MEM
#> 16  MSY MEM
#> 17  LGA PHL
#> 18  PHL PHL
#> 19  PHX LAX
#> 20  PIT PHL
#> 21  STL MEM
#> 22  SFO LAX
#> 23  SEA LAX
#> 24  TPA MEM
#> 25  DCA PHL

We can plot them on a map:

if (!require(tidyverse)) install.packages("tidyverse", dependencies=TRUE)
if (!require(ggplot2)) install.packages("ggplot2", dependencies=TRUE)
if (!require(maps)) install.packages("maps", dependencies=TRUE)
library(tidyverse)
library(ggplot2)
library(maps)
connections <- cities %>%
  left_join(cities %>% select(City, Lat, Long), by = c("Hub" = "City")) %>%
  rename(Hub_Lat = Lat.y, Hub_Long = Long.y) %>%
  select(City, Lat = Lat.x, Long = Long.x, Hub, Hub_Lat, Hub_Long)
hubs <- unique(cities$Hub)
hub_connections <- expand.grid(Hub1 = hubs, Hub2 = hubs, stringsAsFactors = FALSE) %>%
  filter(Hub1 < Hub2) %>%  # Evita duplicati e auto-connessioni
  left_join(cities %>% select(City, Lat, Long), by = c("Hub1" = "City")) %>%
  rename(Lat1 = Lat, Long1 = Long) %>%
  left_join(cities %>% select(City, Lat, Long), by = c("Hub2" = "City")) %>%
  rename(Lat2 = Lat, Long2 = Long)
usa_map <- map_data("state")
gg <- ggplot() +
  geom_polygon(data = usa_map, aes(x = long, y = lat, group = group), fill = "white", color = "black") +
  coord_fixed(1.3) +
  xlim(-125, -66) + ylim(25, 50)
gg <- gg + geom_segment(data = connections, 
                        aes(x = Long, y = Lat, xend = Hub_Long, yend = Hub_Lat),
                        color = "blue", alpha = 0.5, size = 1)
gg <- gg + geom_segment(data = hub_connections,
                        aes(x = Long1, y = Lat1, xend = Long2, yend = Lat2),
                        color = "red", alpha = 0.7, size = 1)
gg <- gg + geom_point(data = cities, aes(x = Long, y = Lat), color = "blue", size = 2)
gg <- gg + geom_point(data = cities[solution,], aes(x = Long, y = Lat), color = "red", size = 3)
gg <- gg + geom_text(data = cities, aes(x = Long, y = Lat, label = City), hjust = 1, vjust = 1, size = 3)
gg <- gg + ggtitle("Airlines hubs (cost minimization)") +
  theme(plot.title = element_text(hjust = 0.5, size = 16, face = "bold"))
print(gg)

Airline hubs

Giulio Barcaroli

2024-09-25

Airline hubs

Prepare data

Optimization

Analysis of the solution