R2BEAT Optimization of precision constraints

2026-02-01


Source: vignettes/CVs_optimization.Rmd

Introduction

  1. In a multivariate stratified sampling design procedure, very often the values of the precision constraints (expressed in terms of maximum expected coefficients of variation set on the target estimates) are set taking into account the budget constraints that oblige to a given affordable sample size. This implies that an expert has to fine tune the precision constraints (increasing and decreasing them) until a satisfactory set is determined. When the number of variables and/or domains is not small, this job can be very expensive. To handle this issue, a new function, the “pareto” one, has been developed, in order to determine an optimal solution in terms of precision constraints, given the affordable sample size.

  2. Another issue is related to the characteristics of the allocation of sampling units in the strata: it may happen that it can be very different from the proportional one. In some cases it may be desirable to limit the distance between the two allocations, avoiding the cases of too much oversampling in small strata. It is possible to obtain this, also in this case by changing the precision constraints. To get this result, it is possible to make use of a genetic algorithm, that explores the space of the possible combinations of values of the precision constraints, with the aim of maximizing the coefficient of correlation of the two distributions (optimal and proportional allocations).

Setting

In this study, we assume that the affordable sample size (given the budget) is set to 50,000. We show how it is possible to start from a “neutral” set of precision constraints (equal CVs for all variables for a given domain level), and modify them, so to:

  • first, balance the influence of all the variables on the determination of the best allocation, or at least, to avoid that only a small fraction plays a role;

  • secondly, get the optimal allocation closer to the proportional one.

We consider a strata dataframe containing information on labor force in a country. Each stratum belongs to three different domain levels:

load("strata.RData")
# strata$DOM3 <- NULL  # de-comment if you want to execute on 2 domains
str(strata)
## 'data.frame':    24 obs. of  18 variables:
##  $ STRATUM      : chr  "north_1_3" "north_1_4" "north_1_5" "north_1_6" ...
##  $ stratum_label: chr  "north_1_3" "north_1_4" "north_1_5" "north_1_6" ...
##  $ DOM1         : chr  "National" "National" "National" "National" ...
##  $ DOM2         : Factor w/ 3 levels "north","center",..: 1 1 1 1 1 1 1 1 2 2 ...
##  $ N            : num  92780 105327 200757 53612 102907 ...
##  $ M1           : num  0.748 0.776 0.782 0.776 0.757 ...
##  $ M2           : num  0.227 0.203 0.199 0.203 0.21 ...
##  $ M3           : num  0.0252 0.0214 0.0192 0.0211 0.0329 ...
##  $ M4           : num  29464 29364 27095 25726 27749 ...
##  $ S1           : num  0.434 0.417 0.413 0.417 0.429 ...
##  $ S2           : num  0.419 0.402 0.399 0.402 0.407 ...
##  $ S3           : num  0.157 0.145 0.137 0.144 0.178 ...
##  $ S4           : num  29839 27542 23575 19557 24520 ...
##  $ CENS         : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ COST         : num  1 1 1 1 1 1 1 1 1 1 ...
##  $ alloc        : num  360 377 682 191 455 373 759 440 181 233 ...
##  $ SOLUZ        : num  352 368 667 187 444 365 742 431 177 227 ...
##  $ DOM3         : chr  "north_1_3" "north_1_4" "north_1_5" "north_1_6" ...

We consider as target variables:

target_vars <- c("active","inactive","unemployed","income_hh")
target_vars
## [1] "active"     "inactive"   "unemployed" "income_hh"

We initially set the following precision constraints:

# De-comment if you want to execute on 2 domains
# cv_equal <- as.data.frame(list(DOM = c("DOM1","DOM2"),
#                          CV1 = c(0.05,0.05),
#                          CV2 = c(0.05,0.05),
#                          CV3 = c(0.05,0.05),
#                          CV4 = c(0.05,0.05)))
# De-comment if you want to execute on 3 domains
cv_equal <- as.data.frame(list(DOM = c("DOM1","DOM2","DOM3"),
                         CV1 = c(0.05,0.05,0.05),
                         CV2 = c(0.05,0.05,0.05),
                         CV3 = c(0.05,0.05,0.05),
                         CV4 = c(0.05,0.05,0.05)))
Coefficients of variation by domain
DOM CV1 CV2 CV3 CV4
DOM1 0.05 0.05 0.05 0.05
DOM2 0.05 0.05 0.05 0.05
DOM3 0.05 0.05 0.05 0.05

and proceed with an initial allocation:

equal <- R2BEAT::beat.1st(strata,cv_equal)

with the following total sample size:

sum(equal$alloc$ALLOC[-nrow(equal$alloc)])
## [1] 137129

Modification of the initial precision constraints to be compliant to the sample size constraint

We now change the initial precision constraints to reach the desired sample size.

To this aim, we make use of the function ‘pareto’. This function determines an optimal set of precision constraints, compliant with the constraint in term of sample size.

Prior to the execution, we set some upper limits to the resulting precision constraints:

caps <- data.frame(
  DOM = c("DOM3"),
  VAR = c("V1","V2","V3","V4"),
  MAX_CV = c(0.10,0.10,0.10,0.10)
)
caps
##    DOM VAR MAX_CV
## 1 DOM3  V1    0.1
## 2 DOM3  V2    0.1
## 3 DOM3  V3    0.1
## 4 DOM3  V4    0.1

In this way, we indicate that whatever solution of the “pareto” function must be such that in DOM3 no CV can exceed these values.

out <- pareto(
  strata = strata,
  current_cvs = cv_equal,
  target_size = 50000,
  tolerance = 5,
  cv_caps = caps,
  beat1cv_fun = beat.1cv_2,
  max_iter = 50,
  max_same_iter = 20,
  plot = TRUE,
  plot_dir = "outputs",
  plot_prefix = "domains",
  show_targets = TRUE,     
  show_caps = TRUE      
)
## Start: t=1.0000000000 -> n=137129 
## Bracket-up: t=1.2500000000 -> n=91446 
## Bracket-up: t=1.5625000000 -> n=60184 
## Bracket-up: t=1.9531250000 -> n=39246 
##   --> Bracket found (t_lo=1.0000000000 infeasible, t_hi=1.9531250000 feasible) 
## Bisect 01: t=1.476562500000 -> n=66988 
## Bisect 02: t=1.714843750000 -> n=50407 
## Bisect 03: t=1.833984375000 -> n=44309 
## Bisect 04: t=1.774414062500 -> n=47213 
## Bisect 05: t=1.744628906250 -> n=48769 
## Bisect 06: t=1.729736328125 -> n=49578 
## Bisect 07: t=1.722290039062 -> n=49988 
## Bisect 08: t=1.718566894531 -> n=50195 
## Bisect 09: t=1.720428466797 -> n=50093 
## Bisect 10: t=1.721359252930 -> n=50041 
## Bisect 11: t=1.721824645996 -> n=50015 
## Bisect 12: t=1.722057342529 -> n=50000
## PNG saved: /home/runner/work/R2BEAT/R2BEAT/vignettes/outputs/domains_nmax_50000_tol_5_t_1.722057_convergence.png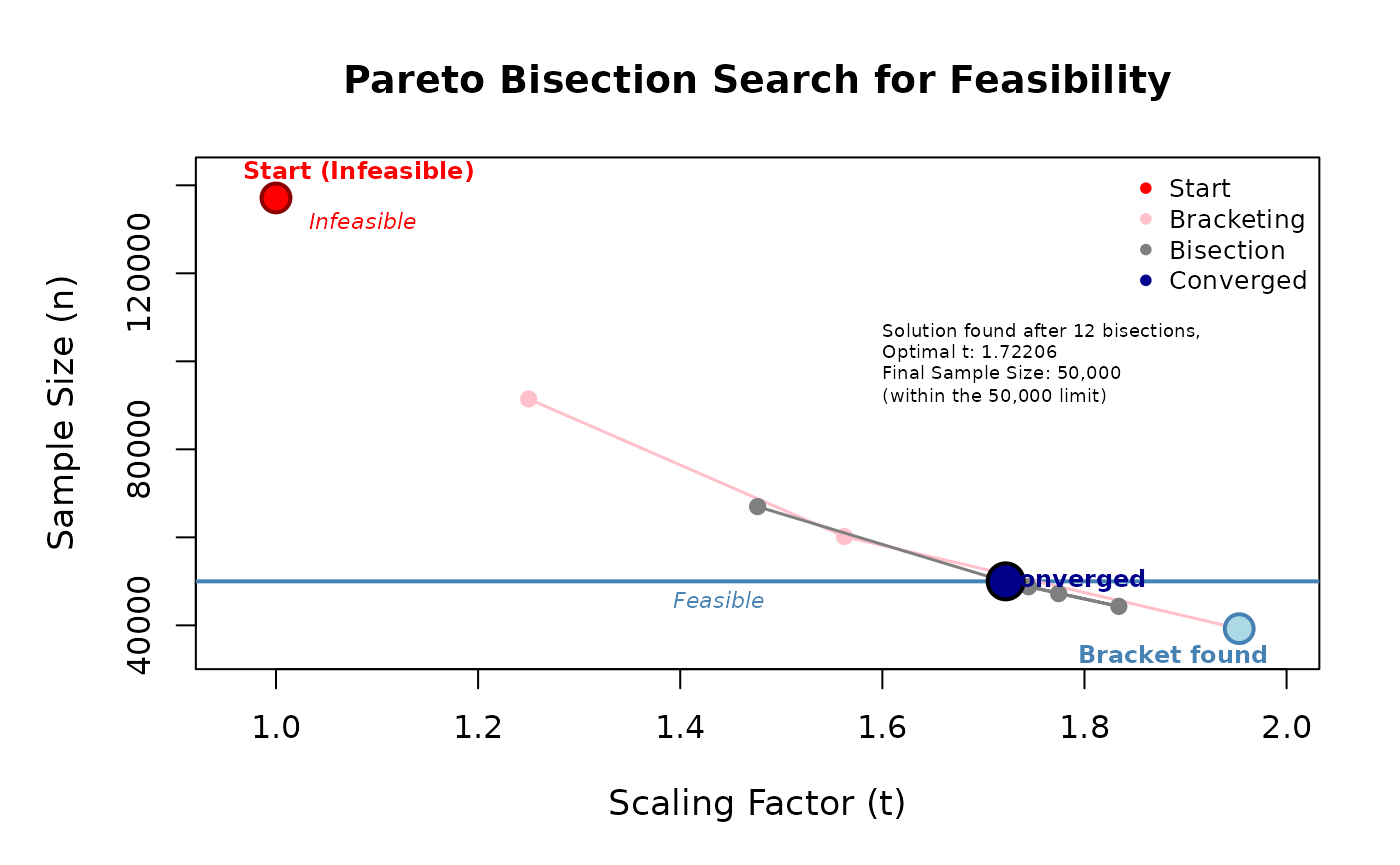

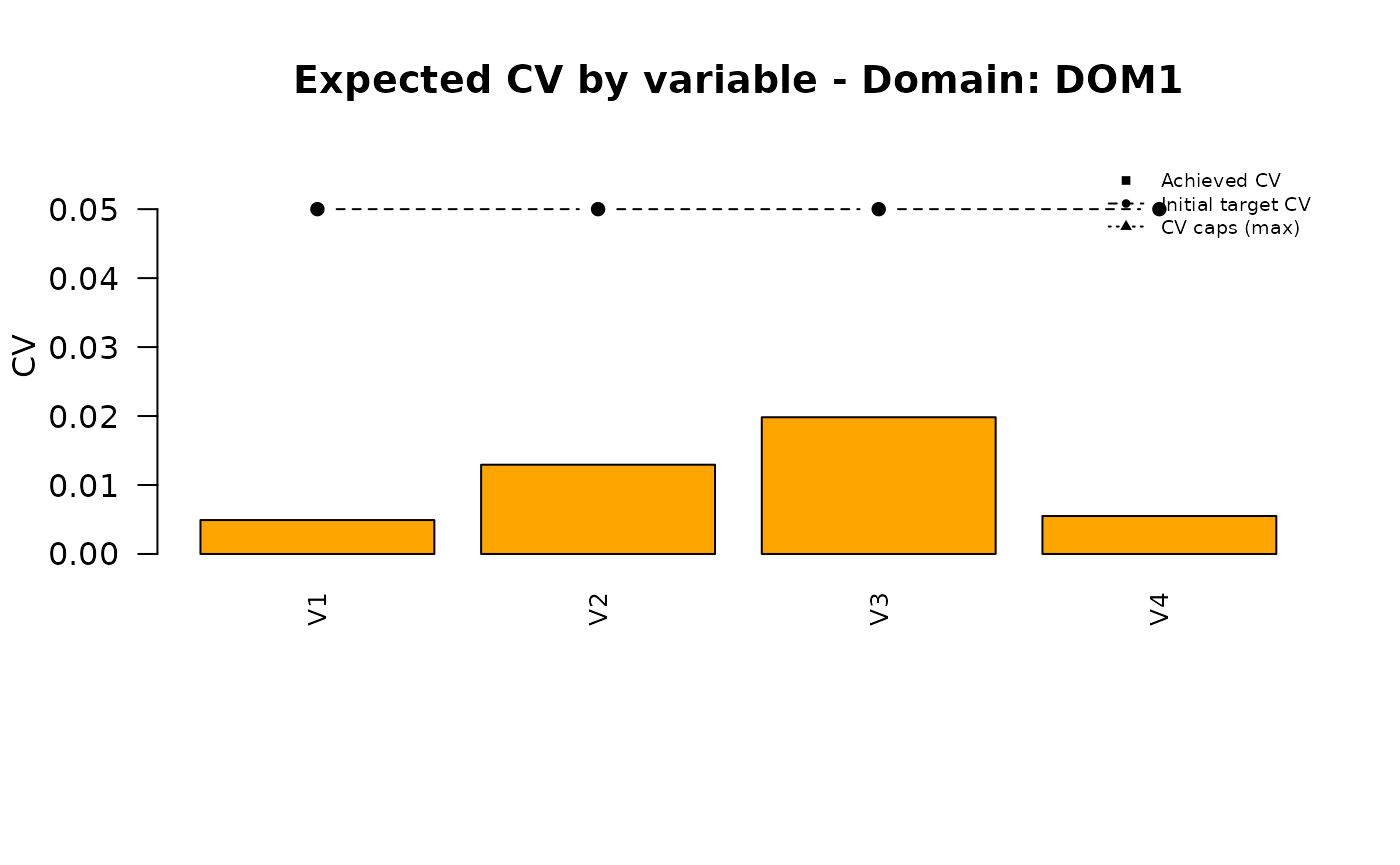
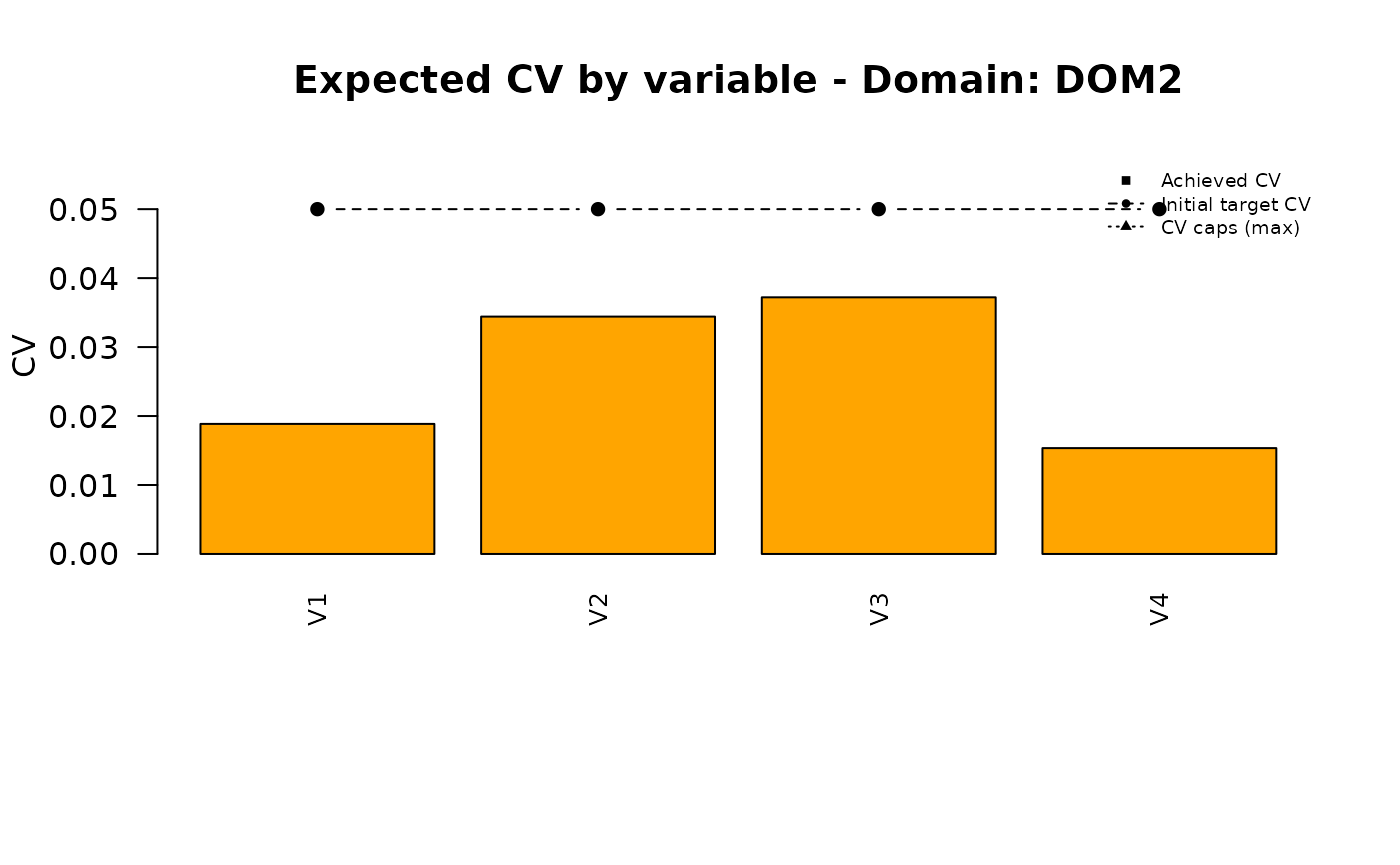
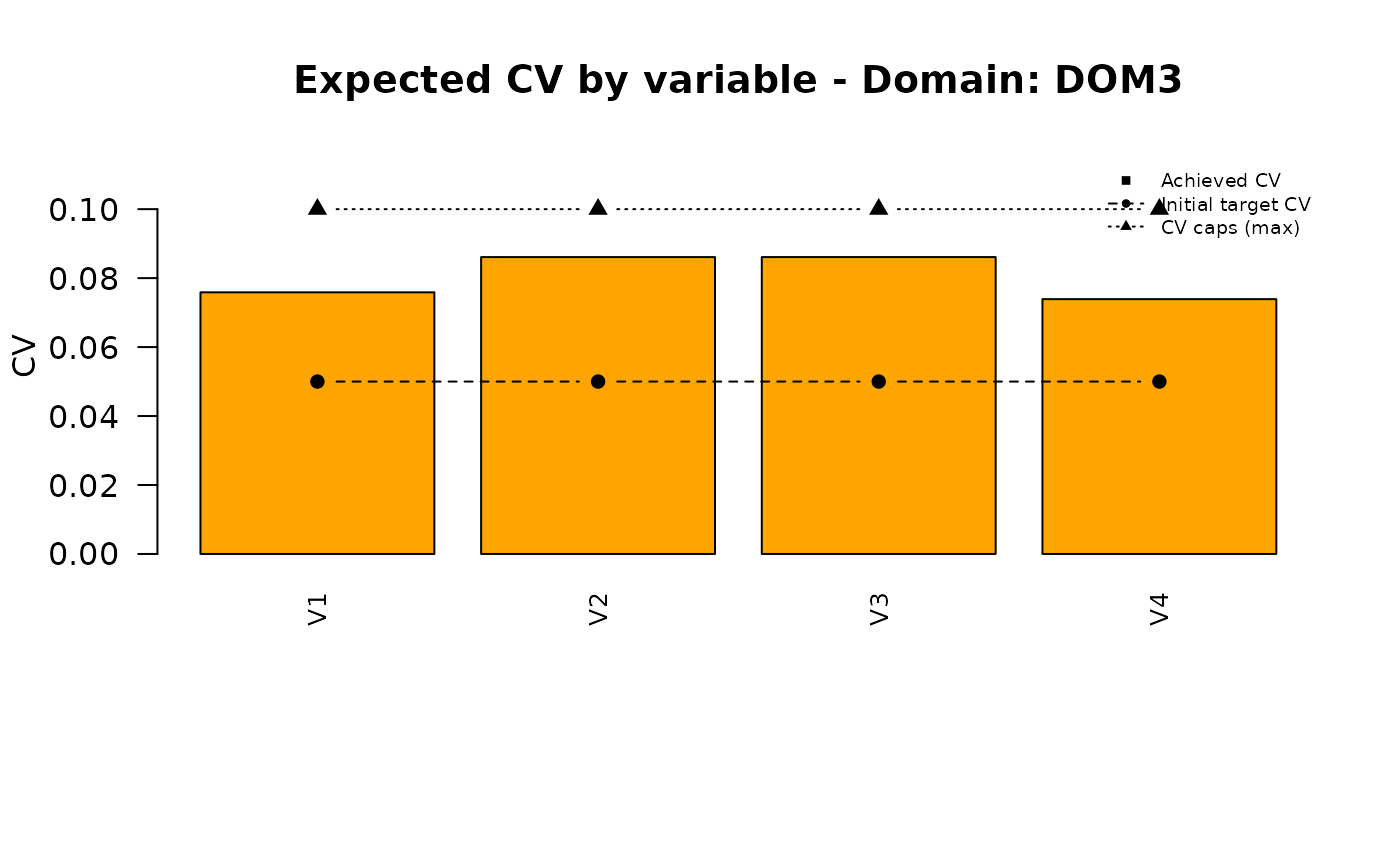
## PNG saved: /home/runner/work/R2BEAT/R2BEAT/vignettes/outputs/domains_nmax_50000_tol_5_t_1.722057_allocation.png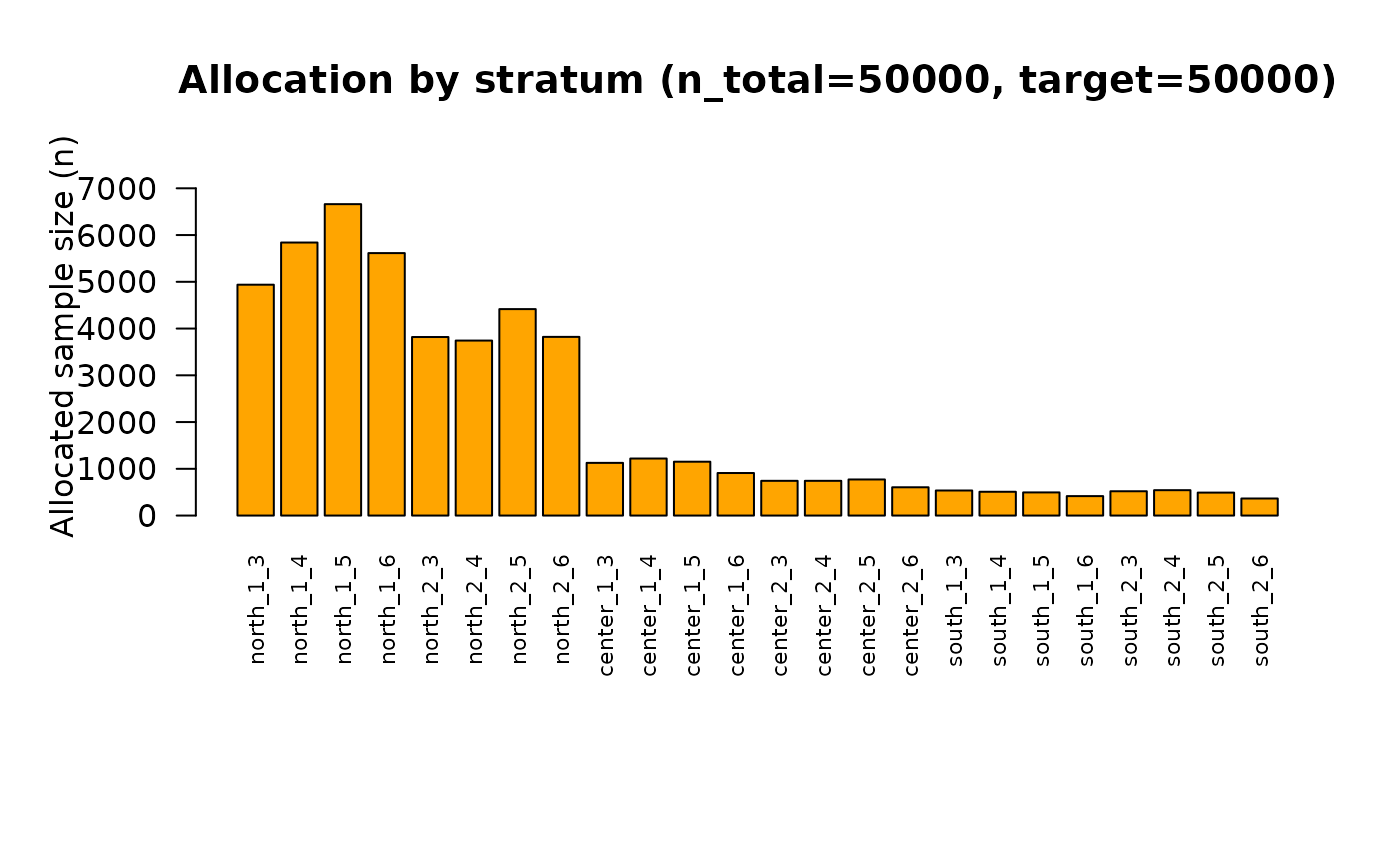

## PDF saved: /home/runner/work/R2BEAT/R2BEAT/vignettes/outputs/domains_CV_and_alloc_nmax_50000_tol_5_t_1.722057342529.pdf

Now, the sample size is in line with the budget constraint:

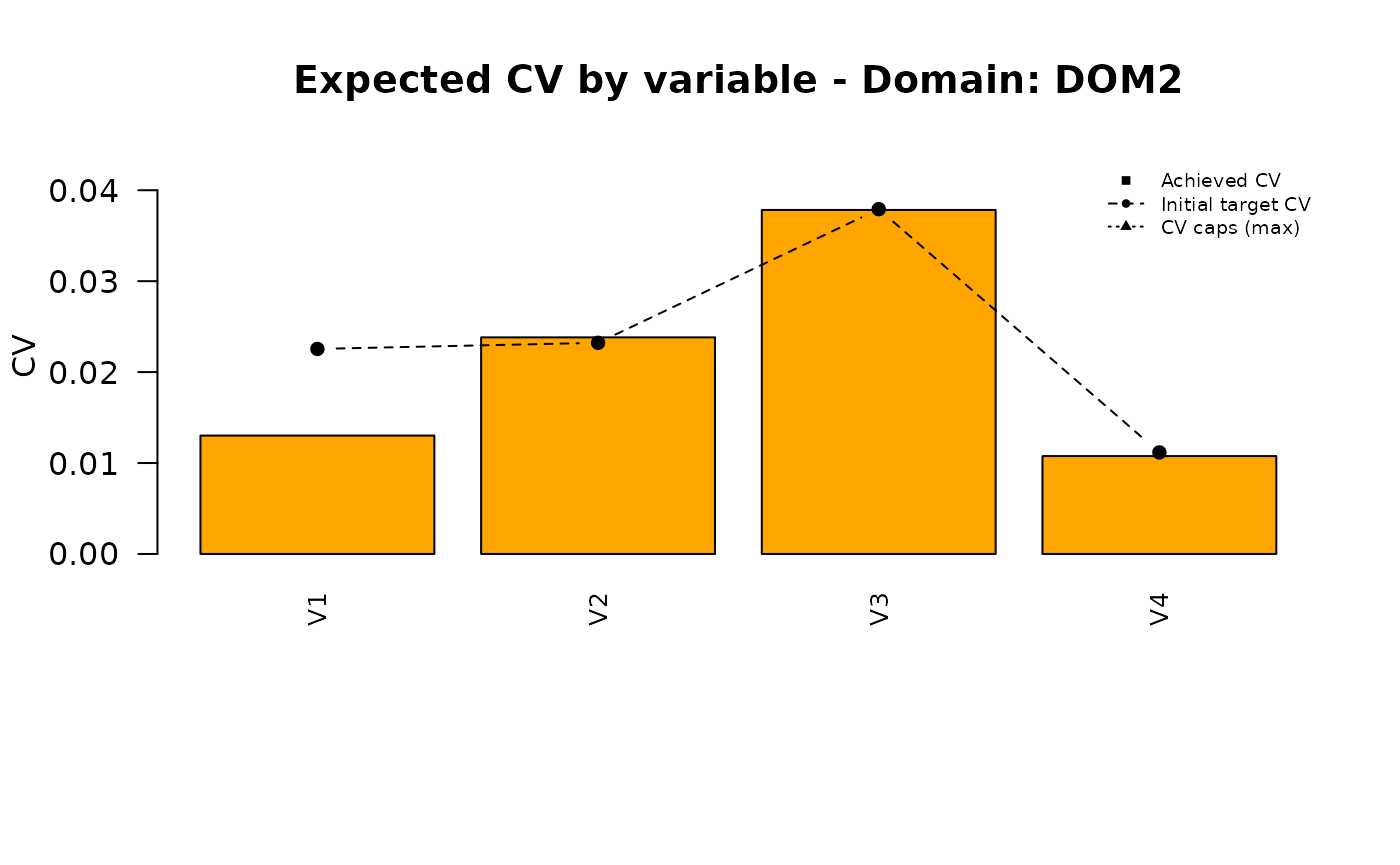
sum(out$allocation$n)
## [1] 50000

These are the new CVs:

cv_pareto <- out$expectedCV 
colnames(cv_pareto)[2:ncol(cv_pareto)] <- paste0("CV",c(1:ncol(cv_pareto)))
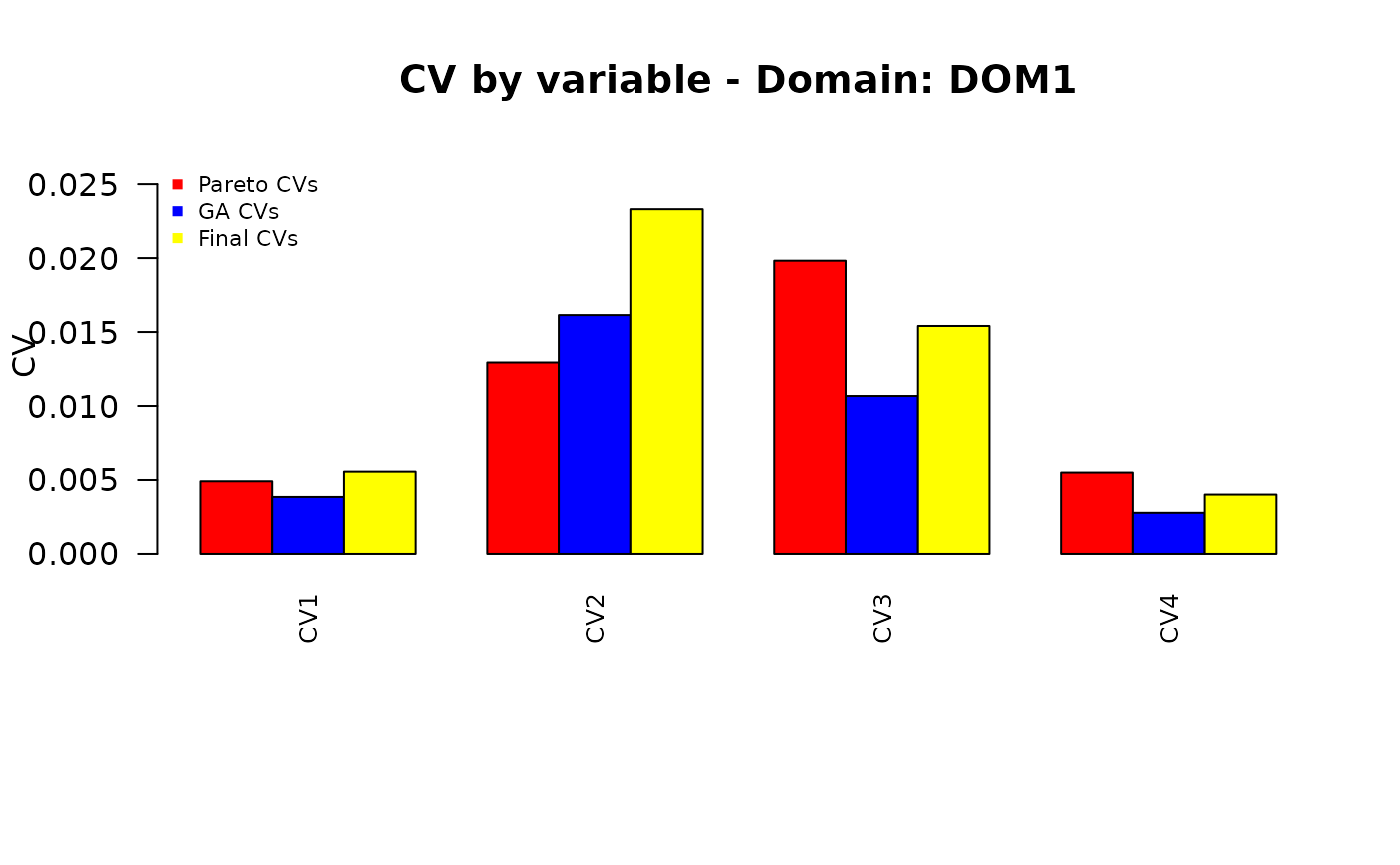
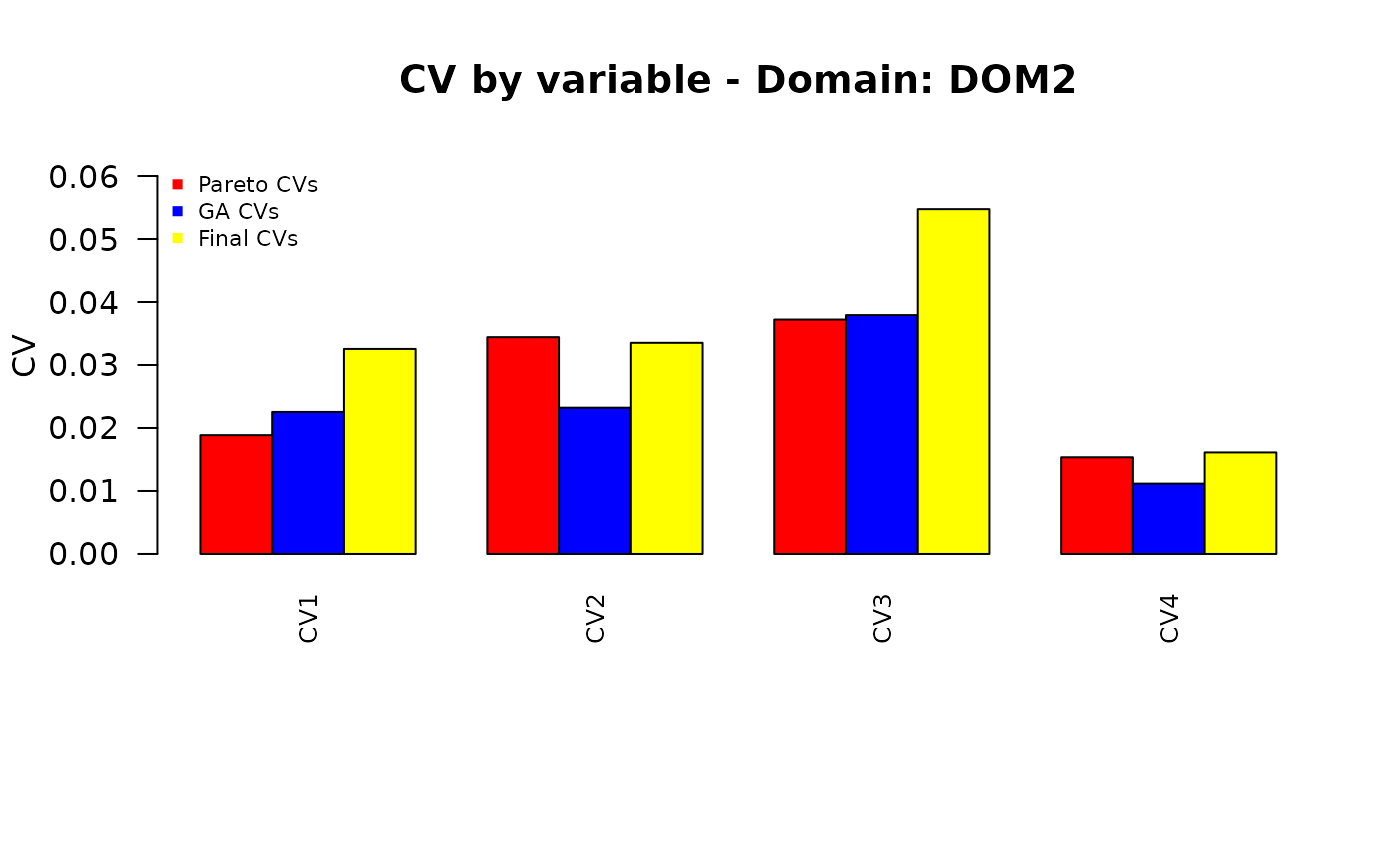
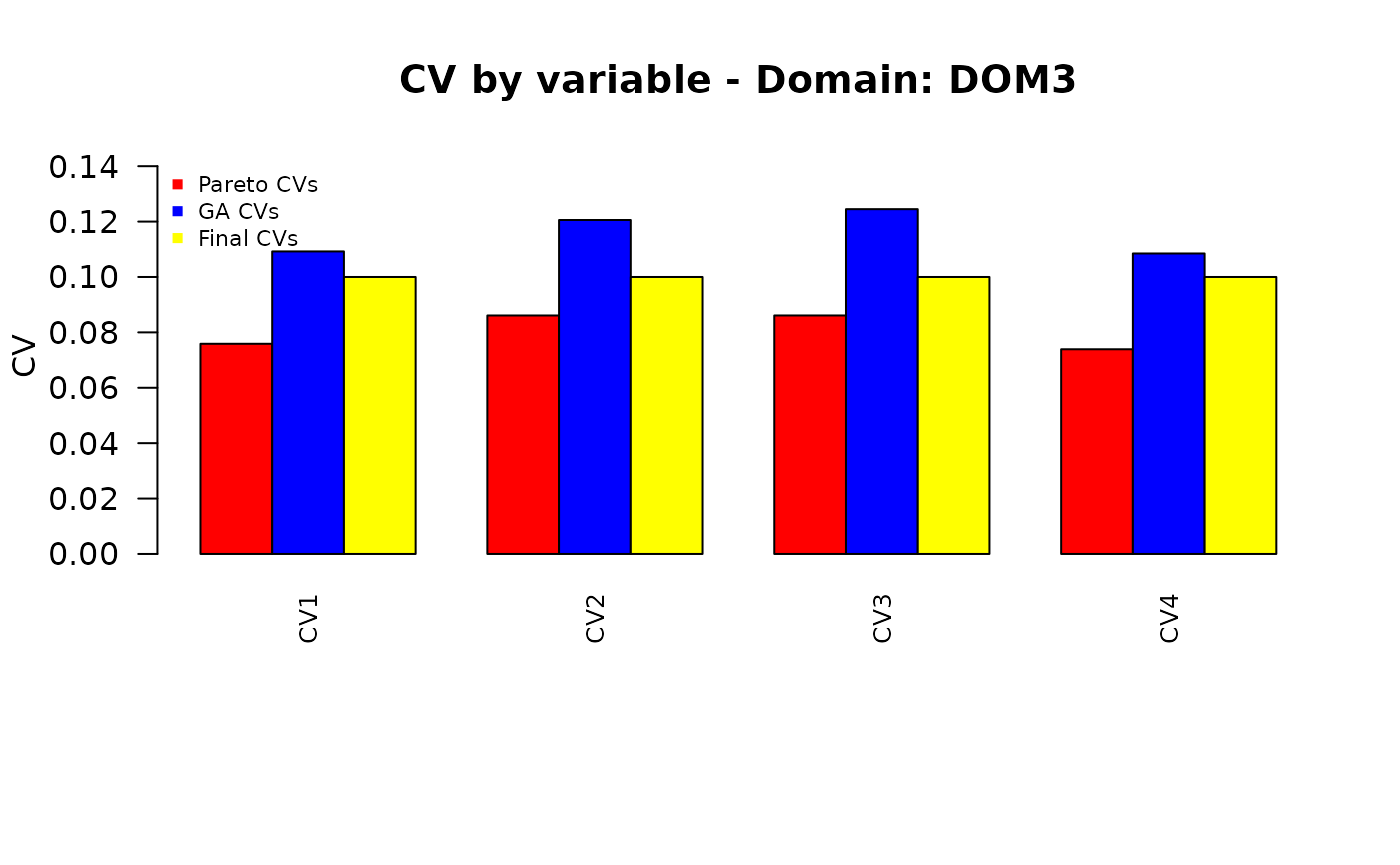
write.table(cv_pareto,"./outputs/2.pareto_cvs.csv",sep=",",quote=F,row.names=F)
Pareto coefficients of variation
DOM CV1 CV2 CV3 CV4
DOM1 0.005 0.013 0.020 0.006
DOM2 0.019 0.034 0.037 0.015
DOM3 0.076 0.086 0.086 0.074

Get the optimal allocation closer to the proportional one

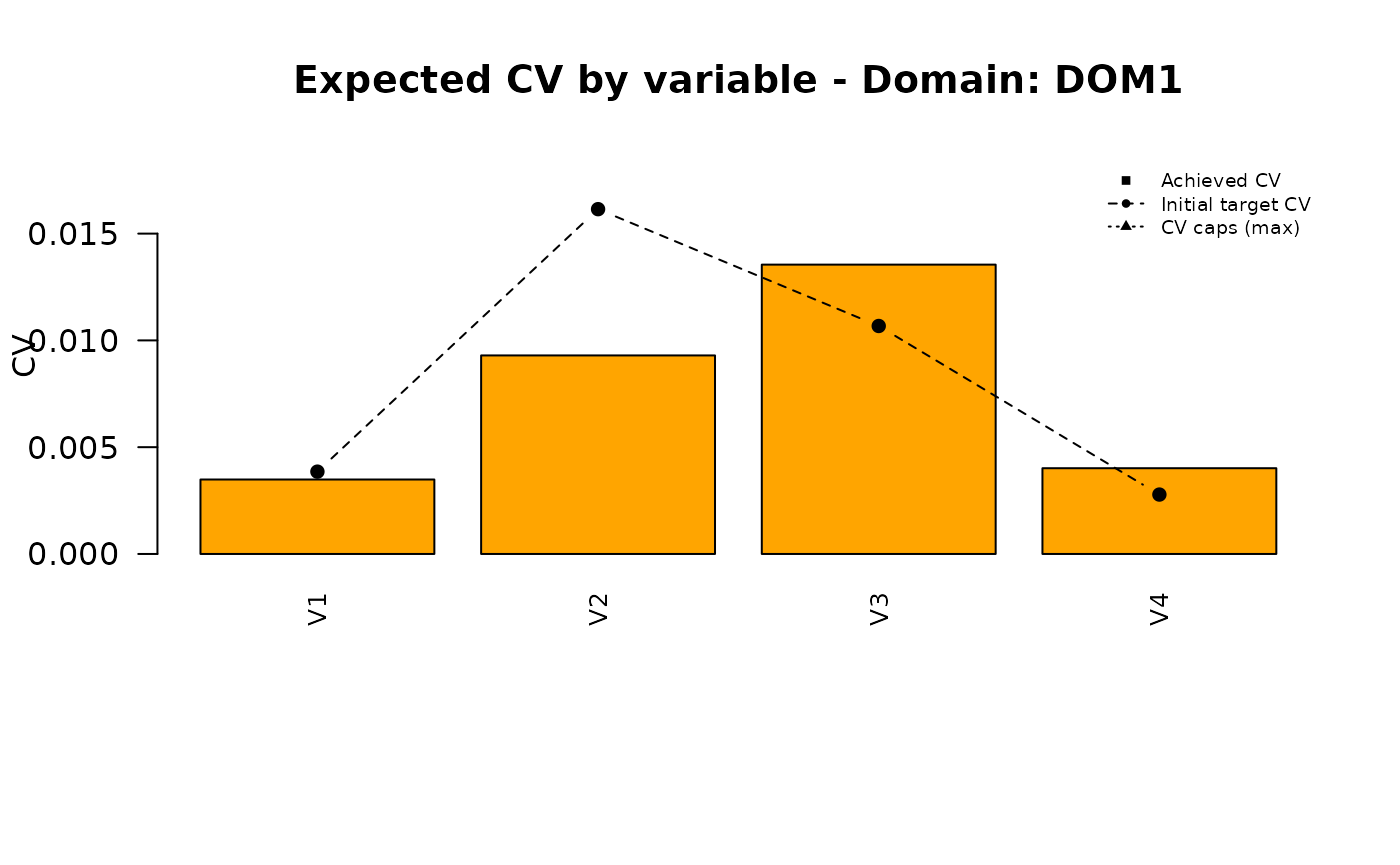
Consider the last obtained solution:

pareto_alloc <- beat.1st(strata,cv_pareto)
knitr::kable(
  pareto_alloc$alloc,
  digits = 3,
  caption = "Pareto allocation",
  format = "html"
) |>
  kableExtra::kable_styling(
    bootstrap_options = c("striped", "condensed"),
    full_width = FALSE
  )
Pareto allocation
STRATUM ALLOC PROP EQUAL
north_1_3 north_1_3 4938 2091.890 2083.417
north_1_4 north_1_4 5840 2374.785 2083.417
north_1_5 north_1_5 6661 4526.424 2083.417
north_1_6 north_1_6 5614 1208.778 2083.417
north_2_3 north_2_3 3819 2320.222 2083.417
north_2_4 north_2_4 3743 1891.698 2083.417
north_2_5 north_2_5 4416 4121.281 2083.417
north_2_6 north_2_6 3822 2249.741 2083.417
center_1_3 center_1_3 1127 4437.004 2083.417
center_1_4 center_1_4 1220 5871.453 2083.417
center_1_5 center_1_5 1152 2556.196 2083.417
center_1_6 center_1_6 910 352.947 2083.417
center_2_3 center_2_3 743 2278.037 2083.417
center_2_4 center_2_4 743 1060.510 2083.417
center_2_5 center_2_5 772 668.986 2083.417
center_2_6 center_2_6 605 563.331 2083.417
south_1_3 south_1_3 536 1377.992 2083.417
south_1_4 south_1_4 509 1664.088 2083.417
south_1_5 south_1_5 496 3097.838 2083.417
south_1_6 south_1_6 416 1286.587 2083.417
south_2_3 south_2_3 520 1238.405 2083.417
south_2_4 south_2_4 543 932.580 2083.417
south_2_5 south_2_5 492 1596.560 2083.417
south_2_6 south_2_6 365 234.667 2083.417
Total 50002 50002.000 50002.000

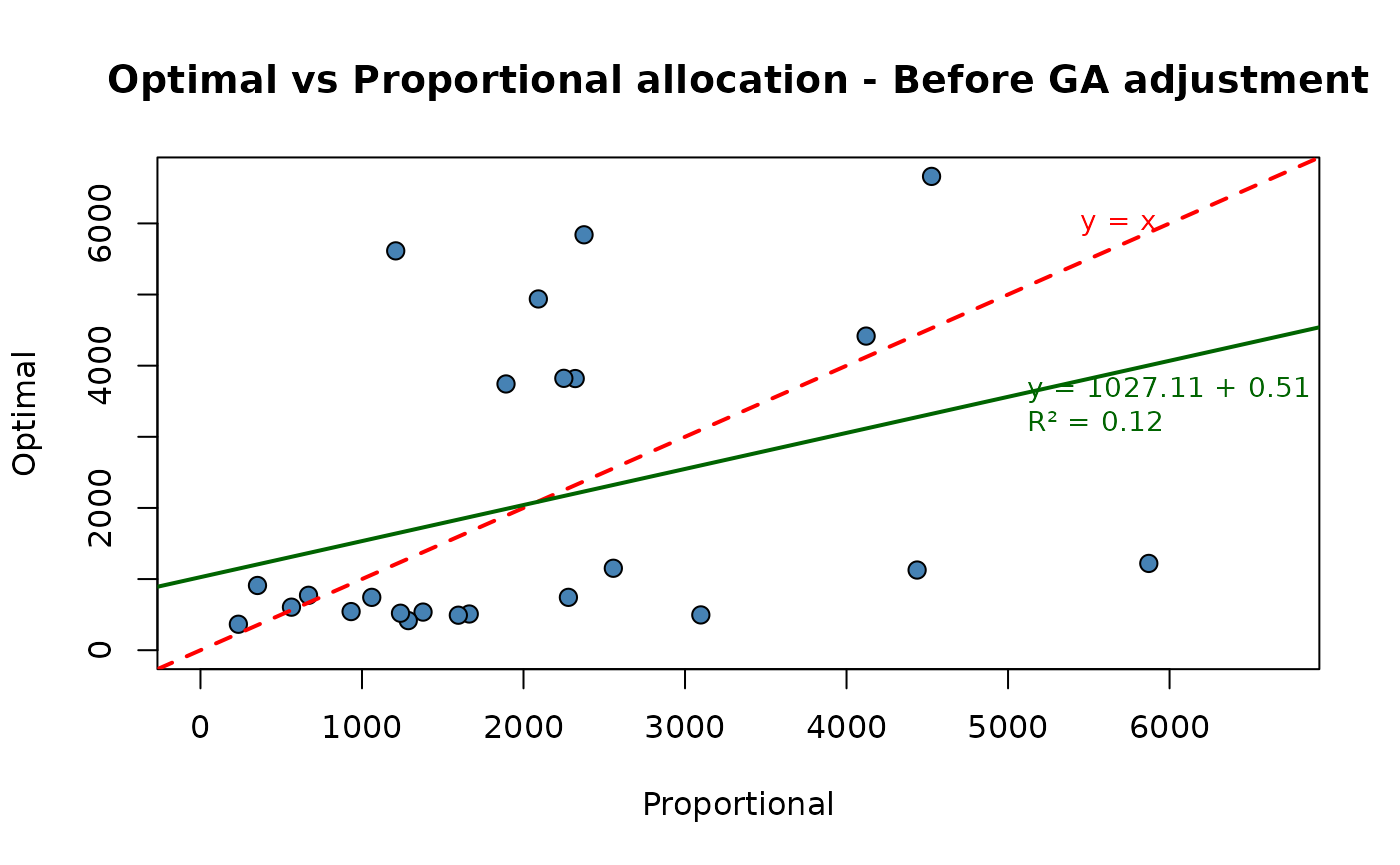
We can calculate the Pearson correlation coefficient between the optimal and proportional allocations:

cor(pareto_alloc$alloc$ALLOC[-nrow(pareto_alloc$alloc)],pareto_alloc$alloc$PROP[-nrow(pareto_alloc$alloc)])
## [1] 0.3467993

We want to get the optimal allocation closer to the proportional one. For instance, we want that the correlation coefficient be increased to 0.95.

To obtain this result, we make use of a particular genetic algorithm, the quantum genetic algorithm, implemented in the R package ‘genalg’.

First, we define the following fitness function:

fitness_cvs <- function(solution) {
  limit <- 0.95   #Insert here the desired correlation
  n_dom <- nrow(cv_pareto)
  n_vars <- ncol(cv_pareto) - 1
  if (length(solution) != n_dom * n_vars) {
    stop("solution length does not match n_dom * n_vars")
  }
  m <- matrix(solution, nrow = n_dom, ncol = n_vars, byrow = TRUE)
  cv_corr <- data.frame(
    DOM = paste0("DOM", 1:n_dom),
    m
  )
  colnames(cv_corr)[2:(n_vars + 1)] <- paste0("CV", 1:n_vars)
  cv_corr
  a <- R2BEAT::beat.1st(strata,cv_corr)
  # b <- ks.test(a$alloc$ALLOC[-nrow(a$alloc)],a$alloc$PROP[-nrow(a$alloc)])
  c <- cor(a$alloc$ALLOC[-nrow(a$alloc)],a$alloc$PROP[-nrow(a$alloc)])
  #---------- Fitness function ----------------
  if (abs(c) > limit + 0.005) c <- 0
  fitness <- -c # genalg always minimizes, so we invert the sign
  return(fitness)
}

The, we set the parameters required by the optimization function (rbga):

nvars <- ncol(cv_pareto) - 1
vett <- NULL
for (k in c(1:nrow(cv_pareto))) {
  vett <- c(vett,cv_pareto[k,c(2:(nvars+1))])
}
vett <- unlist(vett)
vettmin <- vett * 0.5
vettmax <- vett * 1.5

Some explanations regarding the parameters. The parameters ‘vettmin’ and ‘vettmax’ are fundamental to determine the space of possible solutions.

In fact, consider their values:

vettmin
##       CV1       CV2       CV3       CV4       CV1       CV2       CV3       CV4 
## 0.0024570 0.0064705 0.0099120 0.0027510 0.0094300 0.0172095 0.0186080 0.0076745 
##       CV1       CV2       CV3       CV4 
## 0.0379405 0.0430485 0.0430515 0.0369505
vettmax
##       CV1       CV2       CV3       CV4       CV1       CV2       CV3       CV4 
## 0.0073710 0.0194115 0.0297360 0.0082530 0.0282900 0.0516285 0.0558240 0.0230235 
##       CV1       CV2       CV3       CV4 
## 0.1138215 0.1291455 0.1291545 0.1108515

The values in vettmin are the minimum values that the CVs can assume, while the values in vettmax are the maximum ones.

NOTE: the higher the difference between the current correlation and the desired one, the wider the acceptable intervals of variation of the CVs: in this case we assumed plus and minus 50% for each CV.

ndoms = nrow(cv_pareto)
par(mfrow=c(1,2))
#plot vett
plot(vett, col="black", type="l",xaxt = "n", ylim=c(min(vettmin), max(vettmax)), xlab="", ylab="", main="Region of variation for CVs") # xaxt = "n" disables the xaxis ticks
# Generate the vector of labels
vector_labels <- paste("DOM", rep(1:ndoms, each = nvars), 
                       "_V", rep(1:nvars, times = ndoms), 
                       sep = "")
# xticks
axis(side=1,at=seq(1,length(vett)),labels=vector_labels, las=2, cex.axis=0.5)
# vettmin and vettmax
lines(vettmin, col="red")
lines(vettmax, col="blue")
# add legend
legend("topleft", legend=c("cv_input", "cv_min", "cv_max"), col = c("black", "red", "blue"), lty=1, cex=0.5)
plot(solution_genalg)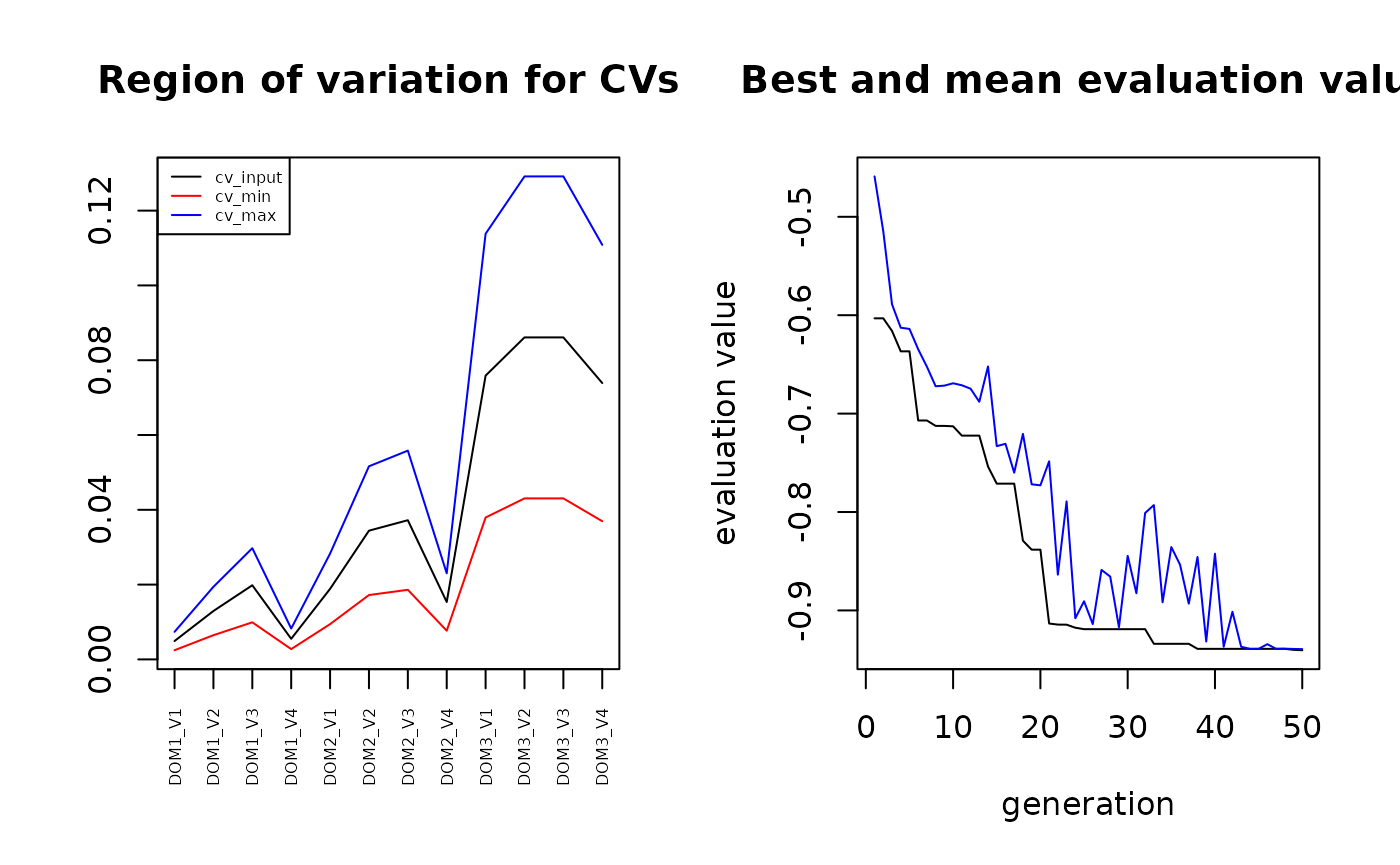

This is the obtained correlation coefficient:

-min(solution_genalg$evaluations)
## [1] 0.9404242

We decode the found solution:

filter = solution_genalg$evaluations == min(solution_genalg$evaluations)
if (sum(filter) > 1) bestSolution = solution_genalg$population[filter, ][1,]
if (sum(filter) == 1) bestSolution = solution_genalg$population[filter, ]
bestSolution
##  [1] 0.003854673 0.016145110 0.010674814 0.002781292 0.022548258 0.023220772
##  [7] 0.037919427 0.011165544 0.109226446 0.120572356 0.124485601 0.108484576
m <- matrix(bestSolution, nrow = ndoms, ncol = nvars, byrow = TRUE)
cv_ga <- data.frame(
  DOM = paste0("DOM", 1:ndoms),
  m
)
colnames(cv_ga)[2:ncol(cv_ga)] <- paste0("CV", 1:nvars)
GA precision constraints
DOM CV1 CV2 CV3 CV4
DOM1 0.004 0.016 0.011 0.003
DOM2 0.023 0.023 0.038 0.011
DOM3 0.109 0.121 0.124 0.108 
ga_solution <- beat.1st(strata,cv_ga)
sum(ga_solution$alloc$ALLOC[-nrow(ga_solution$alloc)])
## [1] 91710
cor(ga_solution$alloc$ALLOC[-nrow(ga_solution$alloc)], ga_solution$alloc$PROP[-nrow(ga_solution$alloc)])
## [1] 0.9404242

Re-execution of the “pareto” function

With these new precision constraints, the sample size is greater than the affordable. So, we apply again the “pareto” function:

out2 <- pareto(
  strata = strata,
  current_cvs = cv_ga,
  target_size = 50000,
  tolerance = 5,
  cv_caps = caps,
  beat1cv_fun = beat.1cv_2,
  max_iter = 50,
  max_same_iter = 20,
  plot = TRUE,
  plot_dir = "outputs",
  plot_prefix = "domains",
  show_targets = TRUE,     
  show_caps = TRUE      
)
## Start: t=1.0000000000 -> n=92650 
## Bracket-up: t=1.2500000000 -> n=62120 
## Bracket-up: t=1.5625000000 -> n=45830 
##   --> Bracket found (t_lo=1.0000000000 infeasible, t_hi=1.5625000000 feasible) 
## Bisect 01: t=1.281250000000 -> n=59627 
## Bisect 02: t=1.421875000000 -> n=50976 
## Bisect 03: t=1.492187500000 -> n=48079 
## Bisect 04: t=1.457031250000 -> n=49430 
## Bisect 05: t=1.439453125000 -> n=50176 
## Bisect 06: t=1.448242187500 -> n=49797 
## Bisect 07: t=1.443847656250 -> n=49985 
## Bisect 08: t=1.441650390625 -> n=50082 
## Bisect 09: t=1.442749023438 -> n=50033 
## Bisect 10: t=1.443298339844 -> n=50010 
## Bisect 11: t=1.443572998047 -> n=49996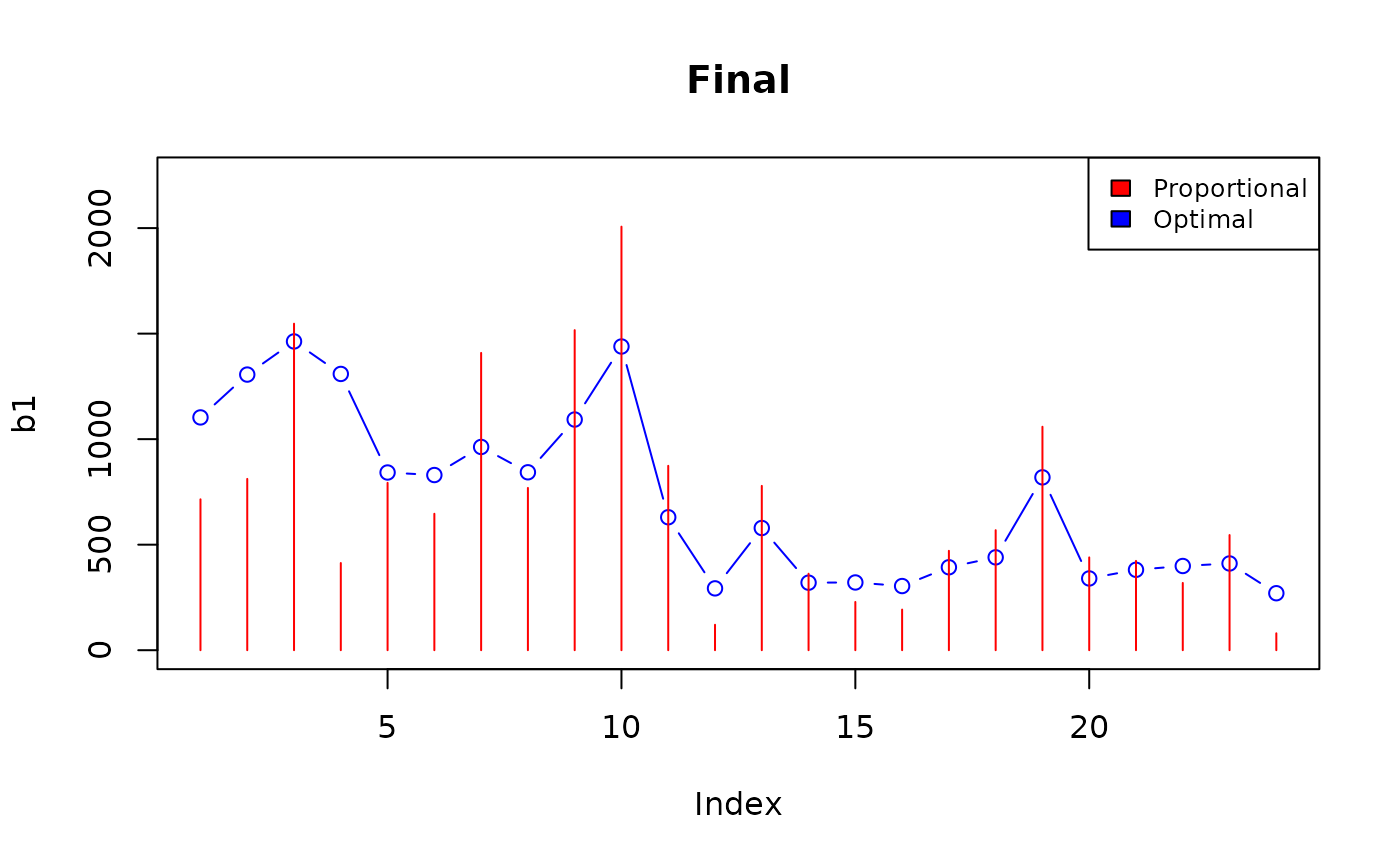

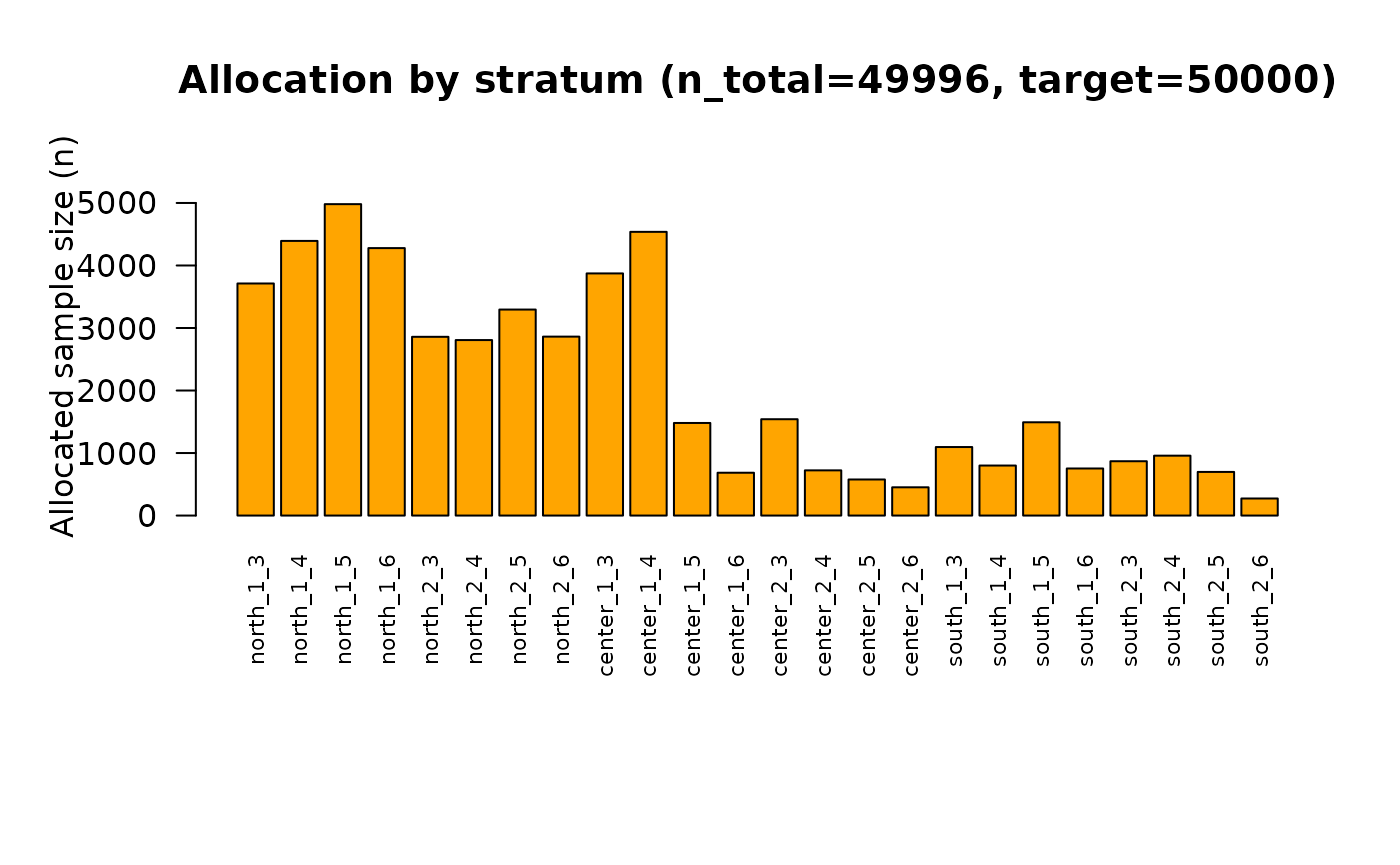
Analysis of the final solution

These is the final set of precision constraints:

cv_final <- out2$errors_scaled
colnames(cv_final)[2:ncol(cv_final)] <- c(paste0("CV",c(1:nvars)))
Final precision constraints
DOM CV1 CV2 CV3 CV4
DOM1 0.006 0.023 0.015 0.004
DOM2 0.033 0.034 0.055 0.016
DOM3 0.100 0.100 0.100 0.100

that produces the following sample size:

final_sol <- beat.1st(strata,cv_final)
sum(final_sol$alloc$ALLOC[-nrow(final_sol$alloc)])
## [1] 49996

in line with the affordable sample size.

What about the closeness of the final optimal allocation to the proportional one?

df <- pareto_alloc$alloc
df <- df[-nrow(df),]
rng = c(0, max(df$ALLOC,df$PROP))   
p1 <- plot(ALLOC  ~  PROP, 
     data = df,
     main = "Optimal vs Proportional allocation - Before GA adjustment",
     ylab = "Optimal",
     xlab = "Proportional",
     xlim = rng,
     ylim = rng,
     pch = 21,
     bg  = "steelblue", 
     col = "black",
     cex = 1.2)
abline(a = 0, b = 1, col = "red", lwd = 2, lty = 2)
text(
  x = rng[2] * 0.8,
  y = rng[2] * 0.9,
  labels = "y = x",
  col = "red",
  pos = 4,
  cex = 0.9
)
fit <- lm(ALLOC~PROP, data = df)
coefs <- coef(fit)
r2 <- summary(fit)$r.squared
abline(fit, col = "darkgreen", lwd = 2)
text(
  x = rng[2] * 0.75,
  y = rng[2] * 0.5,
  labels = sprintf("y = %.2f + %.2f x\nR² = %.2f",
                   coefs[1], coefs[2], r2),
  col = "darkgreen",
  pos = 4,
  cex = 0.9
)

df <- final_sol$alloc
df <- df[-nrow(df),]
rng = c(0, max(df$ALLOC,df$PROP))   
p2 <- plot(ALLOC  ~  PROP, 
     data = df,
     main = "Optimal vs Proportional allocation - After GA adjustment",
     ylab = "Optimal",
     xlab = "Proportional",
     xlim = rng,
     ylim = rng,
     pch = 21,
     bg  = "steelblue", 
     col = "black",
     cex = 1.2)
abline(a = 0, b = 1, col = "red", lwd = 2, lty = 2)
text(
  x = rng[2] * 0.8,
  y = rng[2] * 0.9,
  labels = "y = x",
  col = "red",
  pos = 4,
  cex = 0.9
)
fit <- lm(ALLOC~PROP, data = df)
coefs <- coef(fit)
r2 <- summary(fit)$r.squared
abline(fit, col = "darkgreen", lwd = 2)
text(
  x = rng[2] * 0.75,
  y = rng[2] * 0.5,
  labels = sprintf("y = %.2f + %.2f x\nR² = %.2f",
                   coefs[1], coefs[2], r2),
  col = "darkgreen",
  pos = 4,
  cex = 0.9
)

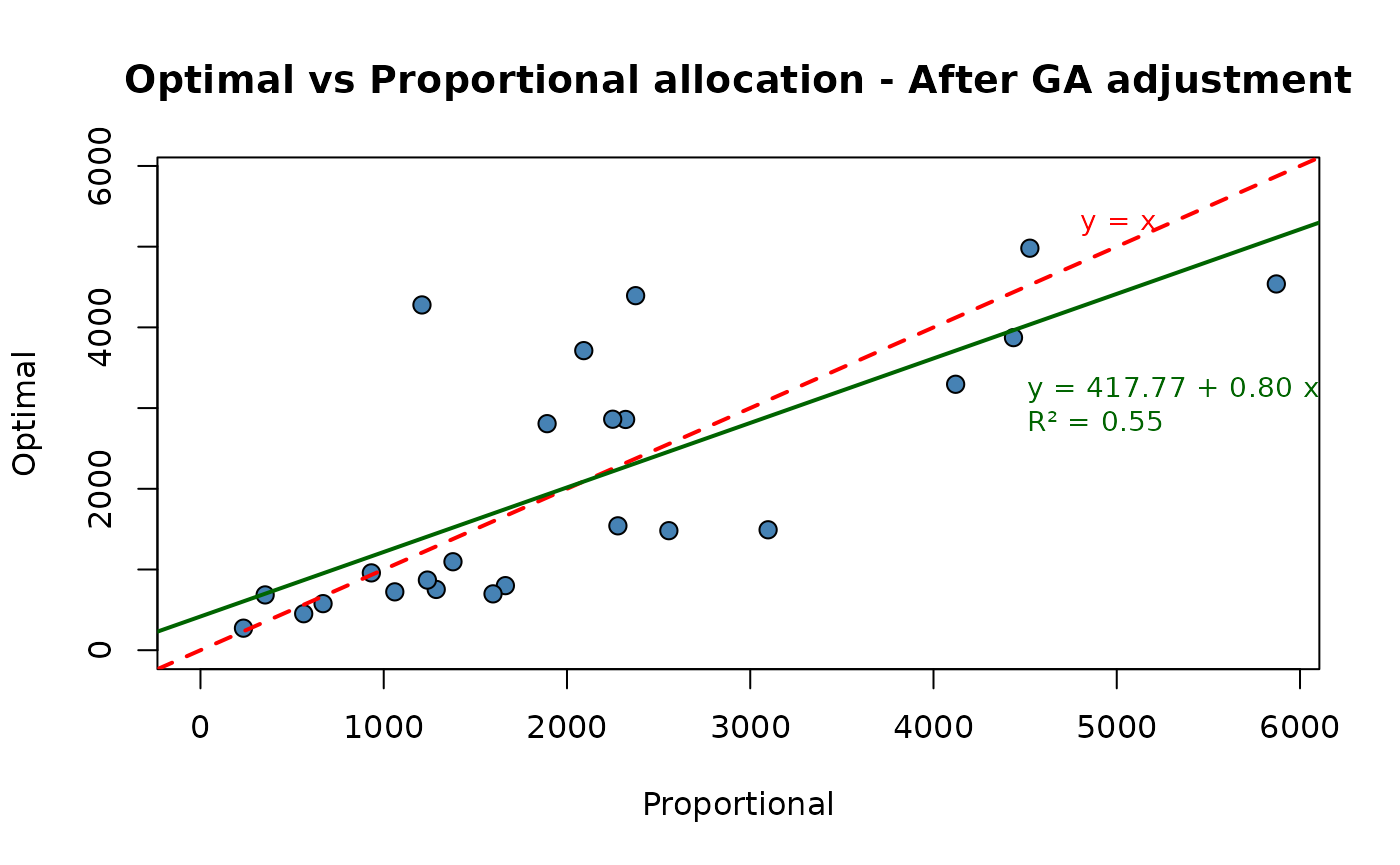So, we obtained a final optimal solution that is much more close to the proportional one with respect to the one obtained with the first application of the “pareto” function.

It is worth noting that the final correlation:

cor(final_sol$alloc$ALLOC[-nrow(final_sol$alloc)],final_sol$alloc$PROP[-nrow(final_sol$alloc)])
## [1] 0.7391439

is not the one that we indicated to and obtained by the genetic algorithm. This is due to the fact that when re-applying the “pareto” function, we lost some of the correlation. If we want a higher value of it we should get back to the genetic algorithm and set a higher value for the desired correlation.

Finally, we want to compare the different sets of the precision constraints:

  • those obtained by applying the “pareto” function to the set of equal CVs;

  • those obtained by applying the genetic algorithm;

  • the final ones, obtained by re-applying the “pareto” function.

plot_domain <- function(dom_label, cv_pareto, cv_ga, cv_final,
                        series_cols = c("red", "blue","yellow")) {
  
  vnames <- names(cv_pareto)
  
  op <- par(no.readonly = TRUE)
  on.exit(par(op), add = TRUE)
  par(mar = c(8, 4, 4, 2) + 0.1)
  
  ymax <- max(cv_pareto, cv_ga, cv_final, na.rm = TRUE) * 1.15
  
  heights <- rbind(Pareto = cv_pareto, GA = cv_ga, Final = cv_final)
  
  bp <- barplot(
    heights,
    beside = TRUE,
    names.arg = vnames,
    las = 2,
    cex.names = 0.8,
    ylim = c(0, ymax),
    main = paste("CV by variable - Domain:", dom_label),
    ylab = "CV",
    col  = series_cols
  )
  
  # bp è una matrice 2 x nvar con le x dei bar; prendiamo i centri del gruppo
  x_centers <- colMeans(bp)
  
  # linea tratteggiata (cv_ga)
  # lines(x_centers, ga_vals, type = "b", lty = 2, pch = 16)
  
  legend(
    "topleft",
    legend = c("Pareto CVs", "GA CVs", "Final CVs"),
    col    = c(series_cols),
    pch    = c(15, 15, 15),
    bty    = "n",
    cex = 0.7
  )
}


doms <- unique(cv_pareto$DOM)
ncols <- ncol(cv_pareto)
vcols <- names(cv_pareto)[2:ncol(cv_pareto)]

for (d in doms) {
  pareto_row     <- cv_pareto[cv_pareto$DOM  == d, vcols, drop = FALSE]
  ga_row <- cv_ga[cv_ga$DOM == d, vcols, drop = FALSE]
  final_row     <- cv_final[cv_final$DOM  == d, vcols, drop = FALSE]
  
  if (nrow(pareto_row) != 1 || nrow(ga_row) != 1 || nrow(final_row) != 1) {
    warning("Dominio ", d, ": righe non univoche nei file. Salto.")
    next
  }
  
  pareto_vals <- as.numeric(pareto_row[1, ])
  ga_vals     <- as.numeric(ga_row[1, ])
  final_vals     <- as.numeric(final_row[1, ])
  
  names(pareto_vals) <- names(ga_vals) <- names(final_vals) <- vcols
  plot_domain(dom_label = d, cv_pareto = pareto_vals, cv_ga = ga_vals, cv_final = final_vals)
}